DE-VAE: Revealing Uncertainty in Parametric and Inverse Projections with Variational Autoencoders using Differential Entropy
IEEE Workshop on Uncertainty Visualization: Unraveling Relationships of Uncertainty, AI, and Decision-Making, 2025.
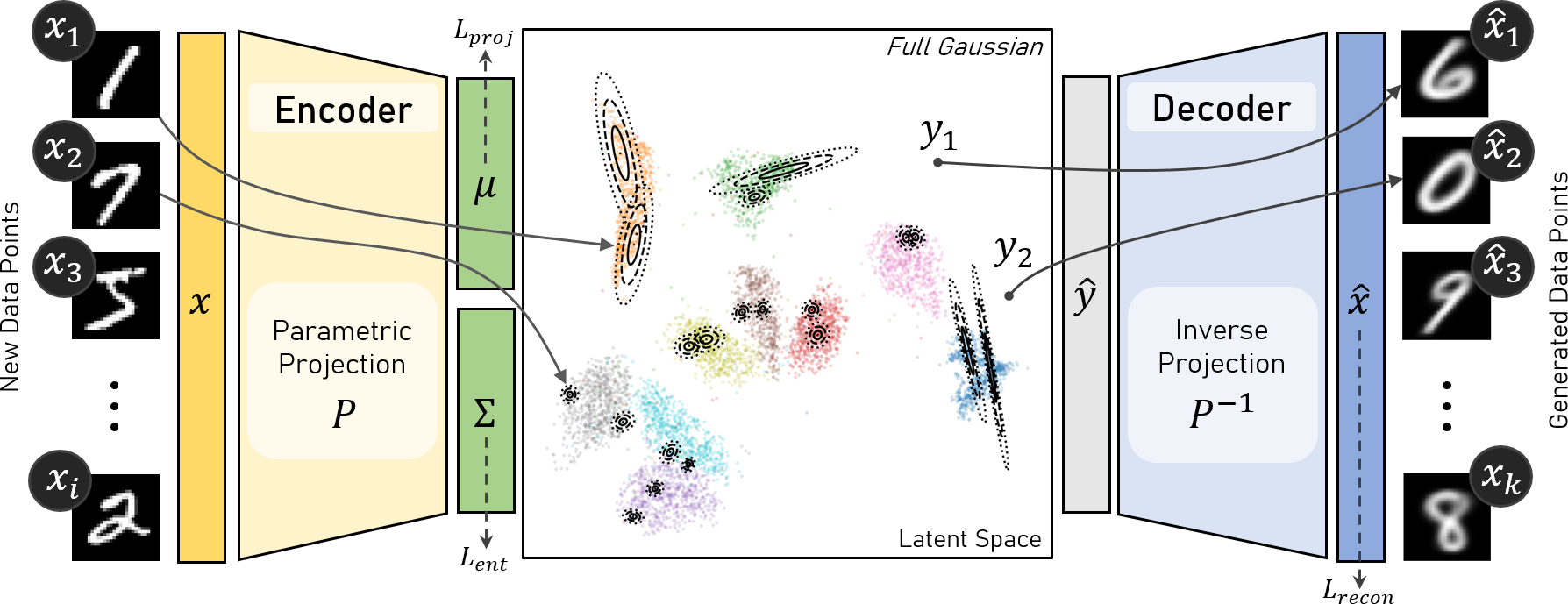
Abstract:Recently, autoencoders (AEs) have gained interest for creating parametric and invertible projections of multidimensional data. Parametric projections make it possible to embed new, unseen samples without recalculating the entire projection, while invertible projections allow the synthesis of new data instances. However, existing methods perform poorly when dealing with out-of-distribution samples in either the data or embedding space. Thus, we propose DE-VAE, an uncertainty-aware variational AE using differential entropy (DE) to improve the learned parametric and invertible projections. Given a fixed projection, we train DE-VAE to learn a mapping into 2D space and an inverse mapping back to the original space. We conduct quantitative and qualitative evaluations on four well-known datasets, using UMAP and t-SNE as baseline projection methods. Our findings show that DE-VAE can create parametric and inverse projections with comparable accuracy to other current AE-based approaches while enabling the analysis of embedding uncertainty.
@inproceedings{Dennig2025DE-VAE,
author = {Dennig, Frederik L. and Keim, Daniel A.},
title = {{DE-VAE: Revealing Uncertainty in Parametric and Inverse Projections with Variational Autoencoders using Differential Entropy}},
booktitle = {{IEEE} Workshop on Uncertainty Visualization: Unraveling Relationships of Uncertainty, AI, and Decision-Making},
publisher = {{IEEE}},
year = {2025},
doi = {10.1109/UncertaintyVisualization68947.2025.00009}
}